[笔记] Integrating Compression and Execution in Column-Oriented Database Systems

原文：Integrating Compression and Execution in Column-Oriented Database Systems

可以与The design and implementation of modern column-oriented database systems对照阅读。

TL;DR

一篇略老（2006年）的paper，但很重要。

数据库中压缩算法的使用是非常影响性能的。这方面列存要比行存更有优势：每列排列在一起天然就适合压缩，而行存中相同列的值是被其它列隔开的。

这篇文章探讨的是，如何在列存数据库中使用压缩，以及不同压缩算法在不同场景中的比较。

Advantages of Column-Stores vs. Row-Stores in Compression

列存相比行存，在压缩方面有以下优势：

列存可以用的压缩算法种类更多。一列的值连续排列，就允许跨行压缩多个值，比如RLE等。此外行存常用的字典等方法仍然可以在列存中使用。
列存的压缩率通常更高。一列的值通常比较类似。
列存的page通常比行存的page更紧凑，扫描时cache命中率更高，CPU消耗更低（尤其是值等大小时），可以使用向量化代码提高解压速度。
列存可以有不同的key order（参考C-Store），而排序好的值更容易压缩。
像RLE这样的压缩算法可以不解压直接操作（比如看到("x", 100)就可以直接选中或淘汰100个值），更是加速了操作。

Graefe和Sahpiro[1])指出了延迟物化的好处，数据在内存中保持压缩状态，只在必要时解压。

Chen等人[2]指出有些算子可以临时性解压来求解谓词，如果有效的话仍然返回压缩数据。

[1]也提出了直接在压缩数据上操作的想法。他们指出如果谓词中的常量部分与数据的压缩方式相同，则可以直接在压缩数据上进行exact-match比较和natural-join。如果使用顺序一致的压缩方式的话，还可以不解压直接做exact-match的index查找。接下来还可以做projection和去重。

但以上工作都没有尝试一个操作同时作用在多个值上，这是本文的贡献之一。

本文的另一个贡献是提出了一种新架构，可以在算子间传递压缩数据，且最小化算子代码复杂度，同时最大化直接在压缩数据上操作的可能。之前的一些工作（[2], [3], [4]）也指出了将压缩本身与更高level的代码隔离的重要性，但通常只是在算子间传递压缩数据，算子内处理前解压。

与Zukowski等人在MonetDB/X100上的工作[5]相比，本文更侧重列存上的压缩算法与压缩数据上的直接操作，而[5]更侧重提升行存上轻量压缩算法的CPU/cache性能。

C-Store Architecture

C-Store的内容可以参考之前的博客，这里简单回顾一下。

C-Store中数据分为RS和WS，RS是全量数据，WS是增量数据，有定期的tuple mover将WS的数据合并进RS。insert会直接写进WS，delete则需要在RS中维护一个标记，update实现为insert+delete。

C-Store的一大特点是数据可以保存为若干个projection，每个projection可以是完整schema的部分列，有自己的sort order（可有多个sort key），很多压缩算法（如RLE）都可以获得更好的压缩效果。不同projection之间通过join index关联。

C-Store的算子是面向列存的，相比传统的面向行存的算子，区别在于：

selection返回bitset，支持高效合并。
有特殊的permute算子可以使用join index来重排序一列。
projection不需要修改数据，因此没有额外开销；两个顺序相同的projection也可以无开销地连起来。
join产生position，而不是value。

Compression Schemes

Null Suppression

Null Suppression的定义参考Wikipedia。它是将数据中的连续的0或空白替换为出现次数和出现位置。本文的实现参考了[4]，但做了如下改动：允许变长字段，方法是在每个值前面附上实际长度。

比如在压缩一组int时，作者不会每个值固定4B，而是用2b编码这个值实际长度，再将所有长度编码保存在一起以保证字节对齐。

Dictionary Encoding

字典编码的定义参考Wikipedia。它是将经常出现的模式替换为对应的更短的编码。

row-store中使用的字典编码通常只能考虑一条记录的值。本文实现的面向列存优化的字典编码则可以考虑多条记录的值。首先计算编码单个值需要的位数X（直接通过distinct数量计算），再计算多少个X位的编码可以放进1-4B中。例如一列有32个值，则X为5，所以1个编码可以放进1B中，3个放进2B，4个放进3B，6个放进4B。假设我们选择3/2，接下来要创建所有可能的3个5b编码与它们的原始值的映射。例如，1、25、31被编码为00000、00001、00010，则字典中会有一项是：

1	X000000000100010 -> 31 25 1

其中X代表未使用的一位。解码过程就很直接了：每读取2B就得到3个值。

注意到我们前面做了字节对齐。即使现代CPU的移位操作已经非常快了，字节对齐仍然能在解码这个CPU性能critical的场合下发挥作用（[5]有类似结论）。

Cache-Conscious Optimization

前面编码组的长度为1-4B，选择时要考虑到L2缓存大小。前面的例子中我们选择了3/2方案，则可能的字典项为32³ = 32768个，因此字典大小为512KB（每项16B，对应3个原始值加上2B的编码也才14B，另外2B不清楚用在哪了）。作者的机器L2缓存为1MB，则512KB刚好是一半。

Parsing Into Single Values

前面的解码过程很容易降级到每次取一个值：用mask与一下就可以了：

1
2
3

(X000000000100010 & 0000000000011111) >> 0 = 00010
(X000000000100010 & 0000001111100000) >> 5 = 00001
(X000000000100010 & 0111110000000000) >> 10 = 00000

很多场合我们可以直接在压缩数据上取出编码值操作，将解压推迟到整个query plan最顶端。

作者实现的字典编码是定长但不保留顺序的，相比保留顺序但变长的方案要有一定性能优势。

Run-length Encoding

RLE的定义参考Wikipedia。它是将连续出现的值替换为三元组：(value, start position, run_length)，其中每个元素都是定长的（因此不能直接用于字符串）。

行存中RLE通常只用于压缩长的字符串，但在列存中RLE有着更广泛的应用，因为一列中经常有连续的值。

Bit-Vector Encoding

Bit-vector encoding的定义参考Wikipedia。它用于cardinality比较小的场景，每个distinct的值对应一个bit-string，长度为这列所有值的数量，其中为1的位代表目标值出现，0代表没出现。如1 1 3 2 2 3 1可以编码为：

1
2
3

1: 1100001
2: 0001100
3: 0010010

这种编码在行存中被用作bit-map索引[6]，有很多关于进一步压缩bit-map和这种压缩对query性能影响的研究。但最近的研究指出[7][8]只在有bit-map非常稀疏（1/1000这个量级）时进一步的压缩才不会阻碍query性能。本文的bit-map只在cardinality很小时使用，此时每个bit-map会比较稠密，因此也没做进一步的压缩。

Heavyweight Compression Schemes

LZ编码可以参考Wikipedia和之前的博客。它有非常多的变种，是使用最广泛的通用压缩算法。

作者选择了LZ算法的一个可以任意使用的版本，针对解压速度有优化。

Compressed Query Execution

Query Executor Architecture

直接在压缩数据上操作可以带来非常明显的性能提升，但如果因此而需要让算子知道具体的压缩类型，就太耦合了，因此作者引入了两个类作为中间层。

第一个类称为compression block，是压缩数据的一种封装。它提供了以下API供算子使用：

有两种方法遍历解压过的数据：调用getNext()会返回一个解压过的值和对应的位置；调用asArray()会返回整个buffer解压过的数组指针。

三个Block Information API都是可以不解压就得到的。重点说下bit-vector encoding，每个compression block只对应一个特定值，因此isPosContig返回false，getSize返回1的数量，getStartValue返回值本身，getEndPosition返回最后一个1的位置。

第二个类是一个新的scan算子，叫DataSource。它作为query plan和存储层之间的接口，知道压缩过的page保存在哪，有哪些索引可用。scan时它会将压缩的page读上来，转换为compression block。对于像LZ这样的重量级算法，DataSource会在读page时直接解压。

有些谓词可以直接下推给DataSource，比如下推equal，且数据是bit-vector编码的，就可以直接返回bit-string。而如果下推equal给字典编码的数据，DataSource会将谓词值转换为字典值再做比较（不用解压数据）。其它时候谓词可以在数据刚从磁盘中读出来时就求值，总之尽可能避免解压。

Compression-Aware Optimizations

考虑一个nested loops join的例子。C-Store中，如果数据已经被组装为tuple了，join就和正常的row-store一样了。但如果数据仍然是列存格式的，join的输出会是两边的position list：

考虑到各种压缩算法，可能伪代码会写成这样：

NLJoin(Predicate q, Column c1, Column c2)
    IF c1 IS NOT COMPRESSED AND c2 IS NOT COMPRESSED
        FOR EACH VALUE valc1 WITH POSITION i IN c1 DO
            FOR EACH VALUE valc2 WITH POSITION j IN c2 DO
                IF q(valc1, valc2) THEN OUTPUT-LEFT: (i), OUTPUT-RIGHT: (j)
            END
        END
    IF c1 IS NOT COMPRESSED AND c2 IS RLE COMPRESSED
        FOR EACH VALUE valc1 WITH POSITION i IN c1 DO
            FOR EACH TRIPLE t WITH VAL v, STARTPOS j AND RUNLEN k IN c2
                IF q(valc1, v) THEN:
                    OUTPUT-LEFT: t,
                    OUTPUT-RIGHT: (j ... j+k-1)
            END
        END
     IF c1 IS NOT COMPRESSED AND c2 IS BIT-VECTOR COMPRESSED
        FOR EACH VALUE valc1 WITH POSITION i IN c1 DO
            FOR EACH VALUE valc2 WITH BITSTRING b IN c2 DO
                // ASSUME THAT THERE ARE num '1's IN b
                IF q(valc1, valc2) THEN OUTPUT
                    OUTPUT-LEFT: NEW RLE TRIPLE (NULL, i, num)
                    OUTPUT-RIGHT: b
            END
        END
    ETC. ETC. FOR EVERY POSSIBLE COMBINATION OF ENCODING TYPES

可以看出为了充分利用不同压缩算法的特点，上面这段代码变得非常繁琐，如果有N种压缩算法，需要写N²种情况。

为了避免这种代码爆炸的情况出现，作者总结了几种压缩算法的特点，提炼为前面的三个Properties API，其中isPosContig()表示这个compression block中的值是否是这列数据中连续的一段。

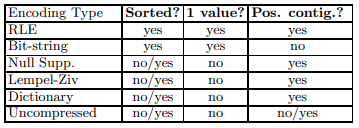
注意上面的表格只对应本文使用的几种实现的特点。

算子可以在无法操作压缩数据时退化到调用getNext()和asArray()来操作解压过的值。我们可以把SELECT c1, COUNT(*) FROM t GROUP BY c1实现为下面的伪代码：

COUNT(COLUMN c1)
    b = GET NEXT COMPRESSED BLOCK FROM c1
    WHILE b IS NOT NULL
        IF b.IsOneValue()
            x = FETCH CURRENT COUNT FOR b.GetStartValue()
            x = x + b.GetSize()
        ELSE
            a = b.AsArray()
            FOR EACH ELEMENT i IN a
                x = FETCH CURRENT COUNT FOR i
                x = x + 1
        b = GET NEXT COMPRESSED BLOCK FROM c1

这段代码中RLE和bit-vector会走同一条路径，从而降低了代码的复杂度。

下图给了更多join和聚合如何使用这几个API的例子。

Experimental Results

Eager Decompression

这项测试的是数据读出来就立刻解压。query很简单：SELECT SUM(C) FROM TABLE GROUP BY C。C列生成了1亿个32位整数。这组测试中C的NDA在2-40之间，模拟一种低cardinality的场景，理论上会比较适合bit-vector。下图是几种压缩算法在不同情况下的压缩后体积。配合这个projection前两列的NDA，我们控制数据的sorted run length为50（图左）和1000（图右），其中C列连续的run length为sorted run length除以它的NDA。

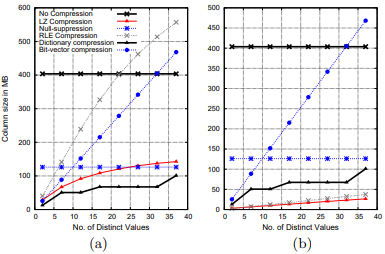
一些结论：

字典和LZ有着最高的压缩率。字典在低cardinality时表现要比LZ好一点。
RLE在run length比较大（低cardinality）时表现良好。
bit-vector的压缩率与NDA呈线性关系。一旦NDA大于32，bit-vector还不如不压缩。

下图是性能对比。

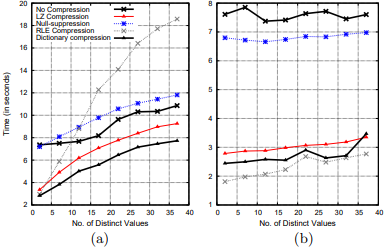
可以看出压缩后体积小不意味着性能好。比如bit-vector体积只有未压缩的一半，但它要比未压缩慢一个数量级（35~120秒，图里没显示）。这也说明解压严重影响了性能，体积小带来的I/O延时优势完全被解压速度淹没了。

bit-vector解压慢是因为它要把并发读多个bit-string再合并起来。RLE和NS比字典和LZ慢是因为它们的解压代码中有比较多的分支，无法充分利用CPU的流水线（[5]有相同结论）。

Operation Directly on Compressed Data

这项测试与上一项的区别在于可以直接在压缩数据上操作。LZ和NS没办法操作，因此它们的性能直接取自上个测试（或忽略）。字典编码有两种直接操作压缩数据的方式，第一种一次取一个编码，局部做group-by得到次数，再将编码替换为真实值乘以次数，得到sum。例如2映射为000，4映射为001，8映射为002。当操作001, 001, 000, 001, 002, 002时，先聚合为001: 3, 000: 1, 002:２，再替换得到结果12, 2, 16。

第二种直接用多个编码值的字典项聚合，然后将所有包含特定值的字典项的聚合值加起来，再乘以真实值。第一种方式适用于所有聚合情况，第二种方式只适用于group-by自身。

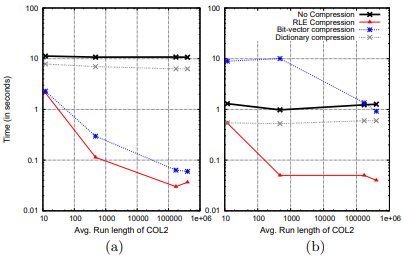
下图a和b是性能对比。

可以看到在sorted run为1000时，RLE相比上一项的性能平均提升了3.3倍，bit-vector则是10.3倍，字典则分别是3.94倍（group-by自身）和1.1倍（group-by非自身）。

图c是在有外界CPU竞争下，测试用时相比图a和b的增加。这里的主要因素是CPU cycle的竞争，而不是cache的竞争。

RLE（run length很短时）和字典的聚合方法一表现不太好，但列存仍然体现出了对行存的优势：一次可以聚合多个值，聚合次数更少了。因此相比于常规压缩的拿CPU换I/O，直接在压缩数据上操作同时节省了I/O和CPU，意味着即使在I/O更快CPU更慢的机器上，压缩加上直接在压缩数据上操作仍然有用。

Higher column cardinalities

下图是更高cardinality时的性能对比。

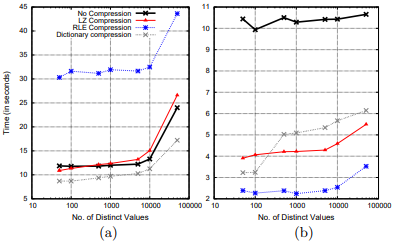
图a的run length为1，图b的run length为14。NS与bit-vector性能太差，图中没显示。注意到cardinality特别大时，hash table已经超过cache大小了，造成了性能的陡降。

注意到RLE和LZ这样依赖于数据局部性的算法在run length为1时表现很差，但run length大一点就有很好的表现。字典则在局部性不好时也有着良好的表现。

下图是几项测试的总结。

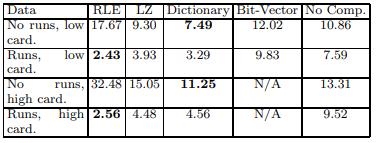
可以看出对于RLE和LZ来说，run length是比cardinality更好的指示器。

Generated vs. TPC-H Data

Other Query Types

这项测试关心一列的压缩是如何影响另一列的访问的。query为：SELECT COL1, COUNT(*) FROM TABLE WHERE PREDICATE(COL2) GROUP BY COL1。

C-Store中会使用position filter来处理这种query，有谓词的列会通过DataSource算子得到一个表示position的bit-string，所有这些bit-string在与/或之后再交给上层算子来取出想要的值。

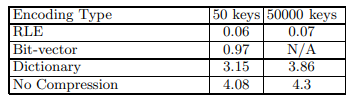
第一个试验使用TPC-H数据，COL2是quantity列（quantity == 1），使用RLE压缩。COL1列可以是suppkey、shipdata、linenumber、returnflag列。使用的projection是按COL1、COL2排序的，因此COL1使用RLE压缩（对有序数据友好）。下图a是结果。

bit-vector这么快是因为它保存的已经是position list了。而且COL1是RLE编码，与bit-string的与操作可以很高效。

第二个试验的query是一样的，但两列的角色交换了下，现在COL1有谓词（仍然是RLE），COL2用来聚合。结果见图b。这个试验中bit-vector表现就不太好了，前面已经提到过它的解压是比较慢的。但在run length很长时，开始出现整个page都是0或1的情况，允许bit-vector做一些优化，表现又变好了。

图a和b的对比说明列该如何编码不光要看数据本身，还要看query类型。一个可能的优化是将相同列以相同顺序但不同压缩方式保存多份。

下一个query是：

SELECT S.COL3, COUNT(*)
FROM P1 AS L, P2 AS S
WHERE PREDICATE(S.COL2) AND PREDICATE(L.COL1)
            AND L.COL2 = S.COL1
GROUP BY S.COL3

这里假设P1是事实表，P2是维度表，projection按S.COL2和L.COL1排序（C-Store会优先按有谓词的列排序projection），因此都使用RLE编码。L.COL2是二级排序列，用来试验不同压缩方式。结果如下：

Conclusion

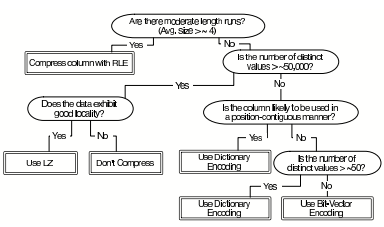
上图总结了用于选择编码的决策树。

其中“exhibits good locality”意思是这列要么已排序，要么与已排序的列有关系，要么数据本身有重复pattern。“likely to be used in a position contiguous manner”意思是这列需要与其它列并行读，因此不能乱序。

除了如何使用压缩算法外，以下几点也很关键：

数据库的schema设计需要感知压缩子系统。数据局部性很重要。
如果能直接在压缩数据上操作的话，就值得牺牲一些压缩率，将重量级压缩算法替换为轻量级压缩算法。
优化器在估计cost时需要意识到压缩算法的影响。