Persistent Data Structure Persistent Data Structure,直译就是“持久性数据结构”。根据Wiki定义 ,如果一种数据结构,能保留它每一次被修改前的版本,就可以被称为“持久性数据结构”。而与之相对的就是Ephemeral Data Structure,即“暂存性数据结构”。
C++中,我们熟悉的数据结构大多数都属于暂存性数据结构,比如std::vector,当我们修改了一个std::vector,与之相关的所有已存在的Iterator就失效了,不能再访问了。而如果我们修改了一个持久性数据结构,我们仍然能够访问到它修改之前的版本,比如Iterator(假如有的话)不会失效,不会读到修改后的数据等。从这个角度讲,持久性数据结构也是不可变(Immutable)的。
什么地方需要用到持久性数据结构?
函数式编程语言。它的定义就要求了不能有可变数据和可变数据结构。
并发编程。
(另外,使用Persistent Map/HashMap有助于简化Prototype的实现,也算是一个用途。)
持久性数据结构对Lazy Evaluation也很有帮助:如果一个数据结构是可变的,我们肯定不会放心对它使用Lazy Evaluation。
Persistent Data Structure与并发 并发编程的核心问题是竞争,即不同线程同时访问相同数据。对此我们往往需要用到一些同步手段来保证临界区的原子性,即同时只有一个线程能读出或写入相同的共享数据。
最常见的同步手段就是锁,但锁也会引起一大堆的问题:
死锁。
活锁。
临界区太大导致性能低下。
错误地在临界区外访问数据导致数据竞争。
控制反转。
…
另一种同步手段基于原子操作,从而实现出一套lock-free的数据结构。它的问题在于:
原子操作本质上也是锁(总线锁),因此高并发度时开销还是会很大。
需要非常精细的实现一个lock-free的数据结构,维护难度大,且很难证明其正确性。一些久经考验的数据结构仍然可能存在bug。
而当我们在不同线程间访问相同的持久性数据结构时,我们很清楚其中不会有任何的数据竞争,因为无论其他线程如何修改这个结构,当前线程看到的结构永远是不变的。这不需要异常复杂的实现和同样复杂的测试来保证。
可以认为通过锁和原子操作实现的并发数据结构追求的是“没有明显的错误”,而持久性数据结构则是“明显没有错误”。
而从性能角度,持久性数据结构也并非一定处于劣势。实现良好的持久性数据结构,通常都可以提供一种或多种操作,其时间和空间复杂度与对应的暂存性数据结构相同。且编译器针对持久性数据结构的不变性,往往能给出更优化的目标代码。
如何实现Persistent Data Structure 想要实现一种持久性数据结构,最简单的方法就是“Copy Anything”,即每当我们修改原结构时,实际上我们都创建了一个副本,再在副本上修改。
当然这种方法的缺点也是很明显的:开销太大。
第二种方法是修改时不创建数据的副本,而是保存每次对结构的修改操作,当需要读取的时候再创建数据的副本,再在其上应用每个操作。显然这种方法在读取时的开销非常大。一种改进方案是每K个修改操作创建一次数据副本。
第三种方法是路径复制(Path Copy),即对于基于Node的数据结构,当我们进行修改时,我们会复制路径上经过的Node,直到最终修改发生的Node。这里我们用“构造”代替了“修改”。
目前最常用的实现方法就是路径复制。
垃圾回收与引用计数 持久性数据结构的一个核心思想是为当前每个持有的人保留一个版本,即对于相同的数据可能同时存在多个版本。这样我们就需要有垃圾回收机制,对于每个版本的数据,在没有人持有之后回收掉。
对于C++而言,通常引用计数就足够了。因为持久化数据结构有一个特点:它的引用链一定是无回路的,只有新对象引用老对象,不可能有老对象引用新对象,因此单纯的引用计数就可以完全回收掉所有垃圾数据。
同时,这个特点对Java类的分代GC也是很有好处的。
有位老同志指出:对于非特定的基于引用计数的数据结构,不能使用std::shared_ptr,原因是它的析构是链式递归进行的,C++的编译器不一定能去掉所有的尾递归,可能会打爆栈。一种解法是从Root节点开始,收集后面所有的节点,然后循环析构。
为什么std::map可以递归析构?因为平衡树的析构链长度为lgn,假设系统的栈深度上限为100,需要std::map中有2^100个元素以上才会栈溢出,此时内存早就爆掉了。
Persistent List Persistent List可能是最简单的持久性数据结构。它支持两种基本操作:构造、插入头节点,即:
1 2 3 4 5 6 7 template <typename T>class List {public : List (); List (T val, List tail); ... };
这里我们使用的实现方法就是路径复制:当我们插入或删除或修改List的第N个节点时,我们需要复制前N-1个节点。
因此,插入或删除头节点都是O(1)的开销,而任意位置插入或删除节点则是O(n)的开销。
基本操作 以下是List的一个最简单实现,包括了支持的几个O(1)操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 template <typename T>class List { struct Item { Item (const T& v, const Item* tail) : mValue (v), mNext (tail) {} T mValue; const Item* mNext; }; explicit List (const Item* item) : mHead(item) { public : List (): mHead (nullptr ) {} List (const T& val, List tail): mHead (new Item (val, tail.mHead)) {} bool Empty () const return mHead == nullptr ; } const T& Front () const assert (mHead); return *mHead; } List PushFront (const T& val) const { return List (val, mHead); } List PopFront () const { return List (mHead->mNext); } private : const Item* mHead; };
可以看到这个实现中还没有任何引用计数有关的代码。我们有两种方式来实现引用计数:
使用std::shared_ptr,这样只需要把每个使用const Item*的地方都换成std::shared_ptr<const Item>即可。
自己实现一种侵入式的引用计数基类Reference,并令Item继承自它。
其它列表操作 当我们拥有了一个持久性的List后,我们就可以在其上实现一套函数式的操作:
fmap
filter
foldl/foldr
forEach
实现戳这里 。
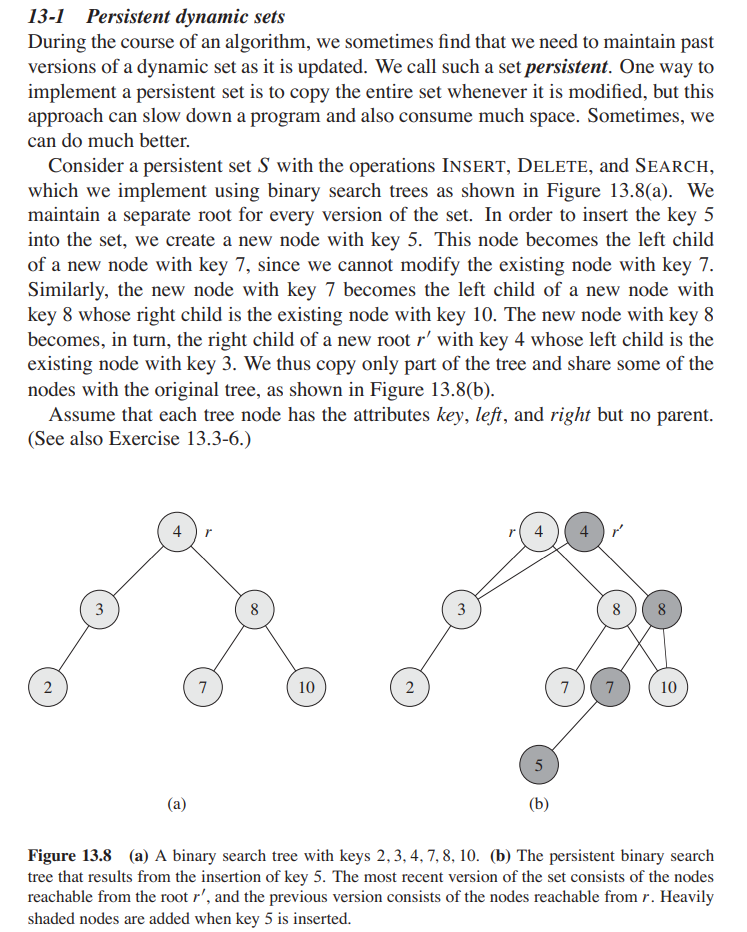
Persistent Map Persistent Map的实现也是基于路径复制的。算法导论上有这么一道习题,清晰的体现了它的实现思路:
当我们插入或删除一个节点时,路径上的每个节点都需要被复制一次,因此这样的操作的开销是O(lgn)的。
插入操作是很简单的:
1 2 3 4 5 6 7 8 9 10 11 Node* Insert (Node* root, const T& val) { if (!root) { return new Node (val, nullptr , nullptr ); } else if (val < root->mValue) { return new Node (root->mValue, Insert (root->mLeft, val), root->mRight); } else if (val > root->mValue) { return new Node (root->mValue, root->mLeft, Insert (root->mRight, val)); } else { return root; } }
删除操作有些麻烦,需要处理删除的节点有子节点的情况。原则就是:用构造代替所有的修改。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Node* Delete (Node* root, const T& val) { if (!root) { return nullptr ; } else if (val < root->mValue) { return new Node (root->mValue, Delete (root->mLeft, val), root->mRight); } else if (val > root->mValue) { return new Node (root->mValue, root->mLeft, Delete (root->mRight, val)); } else { if (!root->mLeft) { return root->mRight; } else if (!root->mRight) { return root->mLeft; } else { Node* leftMost; tie (leftMost, root->mRight) = RemoveLeftMost (root->mRight); return new Node (leftMost->mValue, root->mLeft, root->mRight); } } }
注:以上代码均未考虑垃圾回收。
对于红黑树而言,每次它平衡时,同样要复制涉及到的节点。每次平衡最多涉及3个节点,因此平衡的开销是O(1)。
实现戳这里 。不过这个实现没有删除功能。
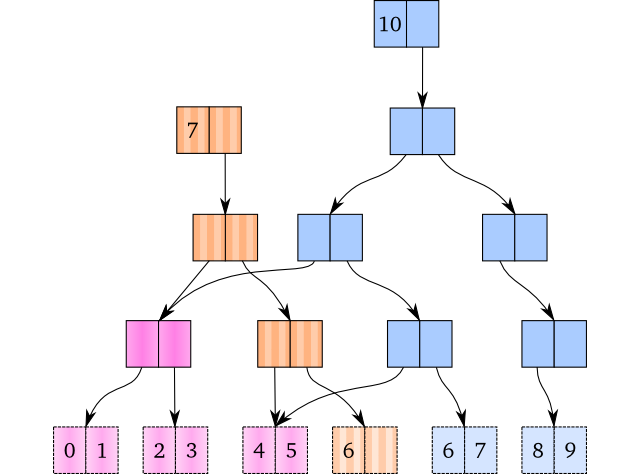
Persistent Vector Persistent Vector的基本思想与Persistent Map非常接近:你把Persistent Vector想象成以下标为Key的Map即可:
图中就是一个这样的Map,它有如下特点:
分为内部节点和叶节点两类,其中数据都在叶节点上。
所有叶节点的高度相同。
每个内部节点有两个子节点。
每层节点中,只有最后一个节点有可能是半满的,其它节点都是满的。
当然这样的实现效率是很低的,每次Update、PushBack的时间复杂度是O(lgn)。因此实践上我们会使用类似于Trie树的结构,即每个节点能容纳多于两个子节点,通常为32个,这样一个6层的Map就可以容纳最多1073741824个元素,每次Update、PushBack最多需要复制6个节点,可以认为变成了一次O(1)操作。
查找:
1 2 3 4 5 6 7 8 const T& Get (Node* root, int32_t index) while (!root->IsLeaf ()) { const int32_t mask = root->Mask (); root = root->Get (index / mask); index %= mask; } return *(const T*)root->Get (index); }
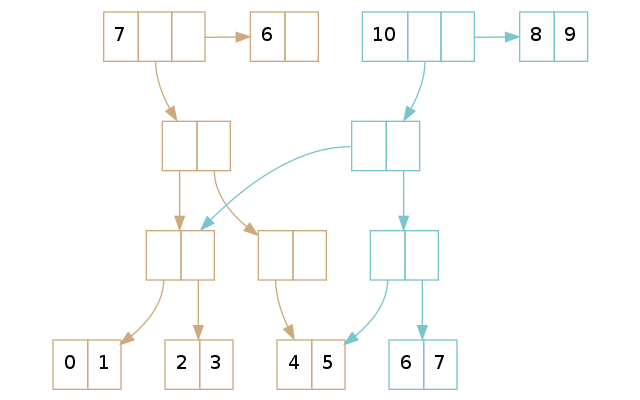
保留Tail节点来提高PushBack性能 想想一个Persistent Vector执行PushBack的时候都发生了什么?从Root开始,一直复制到Tail叶节点。原因是当我们复制了一个子节点,我们就需要修改它的父节点,根据“修改即构造”原则,就需要重新构造一个父节点,从而一直到Root都要构造一遍。
那么,假如Persistent Vector直接持有Tail节点呢?这样当它未满时,PushBack只要复制两个节点:Tail节点和Vector本身。当Tail节点已满时,我们才需要真正做一次PushBack。对于32个子节点的Persistent Vector来说,有31/32的PushBack是真正的O(1)操作,其它1/32的PushBack才需要O(lgn)。
新的查找也很简单。为了配合查找,我们要记录下Tail节点的offset:
1 2 3 4 5 if lookup_index < tail_offset: return tree_lookup(lookup_index) else : return tail[lookup_index - tail_offset]
Transient 当我们要对Persistent Vector进行一系列修改时,每次Update/PushBack/PopBack都要复制lgn节点,即使有了Tail节点优化,也只能对PushBack和PopBack有一定的效果。问题在于,我们即使每个操作都复制了一个新节点,下次操作这个节点时还是要再复制,因为我们要保证不破坏其它人的使用。那么什么时候可以直接重用这个节点,不用复制呢?
只能被当前Vector访问到的节点。
当前Vector在这次操作后不会被其它人使用。
对于条件1,很好解决:我们每次修改Vector时都申请一个UUID,并放到这次修改创建的节点中,这样通过UUID就能判断节点是不是当前Vector创建出来的。
对于条件2,我们没有办法阻止用户在所有修改完成之前使用这个Vector。因此我们使用一个新类型Transient来进行批量修改。好处:显式的让用户知道,我们要做一些不一样的事情啦,在它结束之前不要访问这个Vector。
在批量修改结束之后,还需要一个操作来把Transient变为Persistent,这步操作会把每个节点中的ID置为NULL,保证合法的Vector的节点没有ID,从而避免一个Transient被误用。
Persistent HashMap 当我们有了一个Persistent Vector的实现之后,实现一个Persistent HashMap也就不困难了。
一个HashMap是什么?如果我们使用分桶链表来实现HashMap,它就是一个Vector,其中每个元素是一个List。那么我们可以用Persistent Vector + Persistent List来实现Persistent HashMap。如果我们使用开放散列法来实现HashMap,它就是单纯的一个Vector,只要用Persistent Vector来实现就可以了。
Persistent Data Structure的一个使用场景 想象我们有一个UserMap,保存每个UserID和对应的NickName。有两种操作:
NewUser:增加一对新的UserID和NickName。
Update:修改已有UserID对应的NickName。
现在我们用一个Persistent HashMap作为UserMap。有若干个前台线程可以访问和修改UserMap。
最简单的做法:
前台线程获得当前UserMap,称为M0。
前台线程修改UserMap,得到M1。
前台线程将M0替换为M1,原有的M0析构。
只有一个前台线程时,这种用法是没什么问题的。但当我们有多个前台线程时,就会有问题:
线程T1获得M0。
线程T2获得M0。
线程T1修改M0,得到M1。
线程T2修改M0,得到M2。
线程T1将M0替换为M1。
线程T2将M1替换为M2。
结果就是丢了一次数据!实际上这就是一个很经典的RMW操作,先Read,再本地Modify,再Write写回。对于RMW操作,必不可少的操作就是CompareAndExchange,也就是在Write时比较一下原对象有没有在你的Read之后被修改过。如果有的话,需要重试整个RMW操作。
在我们这个场景中,我们需要做的就是每个线程在替换UserMap时确认一下UserMap的最后修改时间是否与自己手上持有的M0的修改时间相同,如果相同才能完成替换,否则就整个操作重来。这种先确认数据是否冲突再写入的操作,就是一种很典型的Transaction。因此我们可以使用STM(Software Transactional Memory)来更规范的使用UserMap:
线程创建Transaction t。
线程通过t获得M0。
线程通过t修改M0,得到M1。
线程通过t替换UserMap为M1。
这个过程中,如果有数据冲突,根据STM的实现不同,可能在不同的地方失败,只有当没有数据冲突时,整个操作才能顺利走下去。
可以看到,当我们使用Persistent Data Structure时,数据冲突的概率决定了它的使用是否高效。上面的例子中,对于全局唯一的UserMap,如果有大量的修改操作同时进行,那么其中只会有非常少量的操作能成功,其它操作都会因为数据冲突而失败。那么我们在使用时,就要考虑能否减少UserMap的粒度,从而降低冲突概率,提高性能。比如,我们将UserMap分成4096个桶,每个桶是一个Persistent HashMap,那么冲突概率就会小很多,整体性能就上去了。
当然,在分桶后,如果有涉及多个UserID的操作,我们就需要一次性原子的替换多个UserMap。这不是一件容易的事情,幸好,STM就是干这个的。这也说明Persistent Data Structure和STM确实是好朋友。
相关链接