0%

[笔记] Cache Craftiness for Fast Multicore Key-Value Storage

发表于 更新于

原文：Cache Craftiness for Fast Multicore Key-Value Storage

TL;DR

大名鼎鼎的 Masstree。

Introduction

开篇第一句话很酷：“Storage server performance matters”。无论什么系统，单机性能永远是非常关键的。毕竟最好的分布式系统就是不要分布（笑）。

面向多核设计的一些关键因素：

  1. 通常读远多于写，因此优化读的性能要比优化写更关键。
  2. 锁不是万恶之源，争抢才是。纯粹的 lockfree 可能难以实现，实现了性能代价也可能很高。在需要原子更新/读取多值时，细粒度锁往往优于 lockfree。
  3. 从 memory-model 角度理解并发操作，避免使用过强的 coherence（如 serializable）。锁本身意味着 serializable，但如果 acquire/release 就能满足要求，那锁就是过强的。
  4. “不要共享”和“immutable”都是提升性能的利器。这往往意味着 copy-on-write 要出场了。lockfree 也经常需要结合 copy-on-write 才能实现。但此时需要仔细设计如何处理写写冲突。
  5. memory stall 已经成为了现代系统的一大性能瓶颈，充分利用 cache 以及 prefetch 是关键。前者意味着良好的数据结构设计，避免跨 cacheline 的原子操作，避免 false-sharing，利用空间局部性；后者则是在主动利用时间局部性。

Masstree 其实也是一个 LSM-like 系统，亮点是它的 in-memory 结构。

TODO

System interface

Masstree 有一套典型的 key-value 接口：

  • get(k)
  • put(k, v)
  • remove(k)
  • getrange(k, n)

其中前三个是原子的，getrange 不是。

Masstree

Masstree 的特点：

  1. 多核之间共享（区别于不同核访问不同的树）。
  2. 并发结构。
  3. 结合了 B+tree 和 Trie-tree。

Masstree 直面的三个挑战：

  1. 能高效支持多种 key 的分布，包括变长的二进制的 key，且之间可能有大量相同前缀。
  2. 为了保证高性能和扩展性，Masstree 必须支持细粒度并发，且读操作不能读到被写脏的共享数据。
  3. Masstree 的布局必须能支持 prefetch 和按 cacheline 对齐。

后两点被作者称为“cache craftiness”。

Overview

Masstree 的大结构是一棵 trie tree。

ART 中提到 trie tree 相比其它 tree 结构的优点是：

  1. 天然的前缀压缩，不需要在叶子节点保存每个完整的 key，节省空间。
  2. 固定 fanout 的 trie tree 能节省 key 之间的比较开销。另外它按下标寻址的特点也天然适合实现 lockfree。

Masstree 选择用 trie tree 的理由大体也是这样。但 trie tree 的一个问题是 fanout 很难确定：

  1. fanout 太小，树的深度太大，查询经历的节点太多，随机访问次数多，性能不高。
  2. fanout 太大，空间浪费严重。

ART 的思路是设计多种 node 大小，加上前缀压缩和 lazy expansion 来降低空间浪费。

Masstree 则使用了另一种思路：选择一个巨大的 fanout（2^64，8 字节），但使用 B+tree 来实现 trie node。这样混搭方案的优点：

  1. 逻辑上仍然是 trie tree，前缀压缩的优点仍然在。
  2. fanout 足够大，避免树太高。
  3. 物理上使用 B+tree，有效避免空间浪费。
  4. 此时 B+tree 面对的只是单个 trie node 的短 key（不超过 8 字节），可以将 key compare 实现得非常高效。

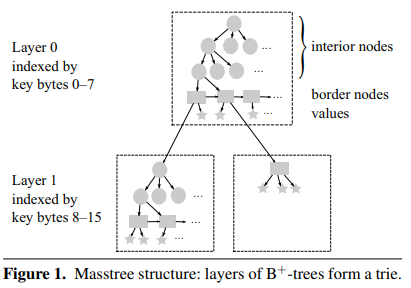
可以看到 Masstree 逻辑上分成了若干层，每层都由多个 B+tree 组成。每个 B+tree 的叶子节点除了存储 key 和 value 外，还可能存储指向下一层 B+tree 的指针。

另外 Masstree 中的 B+tree 内部不会 merge 节点，即 remove key 不会引起 key 的重排。这也是为了避免读路径加锁。

Masstree 同样使用了 lazy expansion，即只在必要的时候创建新的 B+tree。比如一个 key “01234567AB”，长度已经超过了 8 字节，但只要没有其它 key 和它共享前缀 “01234567”，我们就没必须为了它单独创建一层 B+tree。

Masstree 相比普通的 B+tree 的一个缺点是 range query 开销更大，一个是要重建 key，另一个是要遍历更多的 layer。

Layout

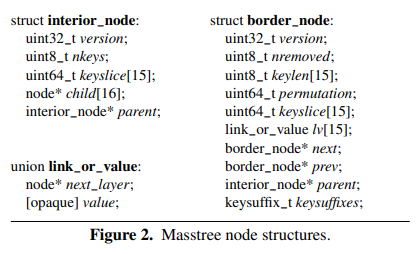
Masstree 中 B+tree 每个节点的 fanout 是 15（精妙的设计），其中所的 border nodes（即 leaf nodes）组成链表以支持 remove 和 getrange。

keyslice 是将长度最多为 8 的 key 编码为一个 uint64（需要保证顺序不变，不足用 0 补齐），这样直接用整数比较代替字符串比较来提升性能。

注意上图中 border node 有 keylen 字段，但 interrior node 就没有了。直接用 keyslice 比较的话必须带上长度，否则无法区分原本就有的 0 和后补上的 0。但 Masstree 保证所有相同 keyslice 的 key 都位于相同的 border node 上，这样 interrior node 上就不需要保存 keylen，直接比较 keyslice 即可，进一步提升了性能。

相同 keyslice 最多有 10 个不同的 key（长度 0-8，外加一个长度可能超过 8 的 key），而 B+tree 的 fanout 是 15，因此总是可以保证这些 key 都在相同的 border node 上。

每个 border node 上所有 key 超过 8 字节的部分都保存在 keysuffixes 中。根据情况它既可能是 inline 的，也可能指向另一块内存。合理设定 inline 大小能提升一些性能。（但不多，可能是因为超过 8 字节的 key 并没有那么多）

所有 value 都保存在 link_or_value 中，其中是 value 还是指向下一级 B+tree 的指针是由 keylen 决定的。

Masstree 在访问一个 node 之前会先 prefetch，这就允许 Masstree 使用更宽的 node 来降低树的高度。实践表明当 border node 能放进 4 个 cacheline 大小（256B）时性能最好，此时允许的 fanout 就是 15。

Nonconcurrent modification

insert 可能造成自底向上的分裂，但 remove 不会合并节点，只有当某个节点因此变空的时候，整个节点一起删掉。这个过程也是自底向上的。

所有 border node 之间维护一个双向链表，目的是加速 remove 和 getrange。后者只要求单向链表，但前者的实现依赖双向链表。

Masstree 有个对尾插入的优化：如果一个 key 插入到当前 B+tree 的尾部（border node 没有 next），且当前 border node 已经满了，则它直接插入到新节点中，老节点的数据不移动。

Concurrency overview

Masstree 中的并发控制本质上是 MVCC + 读路径乐观锁 + 写路径悲观锁：

  1. 每个节点有一个 version 字段，读请求需要在读节点数据的前后分别获取一次 version，确保 version 不变，从而避免脏读。
  2. version 本身包含 lock 以及细粒度的状态信息，写路径通过悲观锁来解决冲突。

其中比较困难的是保证 split 和 remove 时读请求仍然能正确地读到数据。

Writer-writer coordination

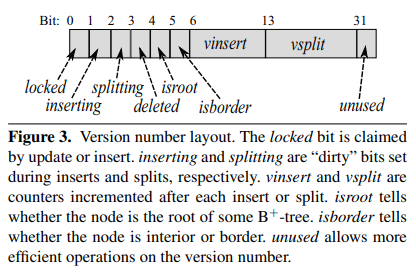
所有对 node 的修改都需要先对 node 加锁，例外：

  • parent 是由 parent node 的锁保护。
  • prev 是由 prev sibling node 的锁保护。

这样可以简化 split 时的状态管理：parent node 可以直接修改 children 的 parent；原有的 node 可以直接修改新 split 出来的 node 的 prev。

split 操作需要同时锁住三个 node：当前 node、parent、next。为了避免死锁，加锁顺序永远是从左向右，从下向上。

这个例子中是先锁 node，再锁 next，再锁 parent。

作者表示曾经对比过不同的并发控制方式，最终决定使用这种细粒度 spinlock 方案。相比之下纯粹使用 CAS 并不会降低 cache 层面的一致性开销。

但使用 Masstree 的应用要自己控制好线程数量，尽量减少 context switch，毕竟使用了 spinlock。

Writer-reader coordination

基本原则：

  1. 一次写操作开始前会修改 version，结束后再修改一次 version。
  2. 读操作开始前会读一次 version，结束后再读一次 version，如果两者不等，说明发生了脏读，需要重试。

接下来的优化方向是：针对部分写操作避免修改 version；针对部分读操作避免重试。

Updates

update 操作会修改已有的 value，需要保证这次修改是原子的。这样不会影响到读操作的正确性，因此也就不需要修改 version。但注意的是写请求不能直接删除一个值，需要用 epoch reclamation 等方法 lazy 回收。

Border inserts

当插入一个值到 border node 上时，为了避免重排已有的 key-value，同时确保这次插入本身对读请求原子可见，Masstree 使用了一种非常巧妙的方法。

每个节点的 key 和 value 数组都是 append-only 的，真正的顺序通过 permutation 字段体现。每个 node 的 fanout 是 15，每个元素用 4 位，这样一共是 60 位，再加上 4 位来表示当前有多少个元素，正好可以放进一个 uint64 中。

完整的插入流程：

  1. 锁住 node
  2. load permutation
  3. 计算得到新的 permutation
  4. append 新的 key-value
  5. 原子写回新的 permutation。直到此时这次插入才对读请求可见。
  6. 释放锁

这个过程不会出现脏读，因此也不需要修改 version。

version 中的 vinsert 不处理 border inserts

New layers

Masstree 会将 layer 的创建推迟到 border node 上两个 key 冲突（回顾前面的 lazy expansion，如果两个 key 映射到相同的 keyslice 上，就意味着需要创建新的 layer 了）。

因此，创建新 layer 必然意味着某个 border node 的 key 已经存在。针对一个 key 的操作都可以不修改 version。但这里有个特殊情况要处理：我们现在要将它对应的 value 替换为一个新的 B+tree。这就意味着我们要完成两项修改（link_or_value 和 keylen），不可能由一个原子操作完成。

为了不修改 version（会导致对其它 key 的读操作重试），Masstree 这里引入了一个中间状态：首先将 keylen 修改为 UNSTABLE，接下来修改 link_or_value，之后再将 kenlen 修改为正确的值。读请求如果遇到了 UNSTABLE 需要自行重试。

又是一个要尽量避免 context switch 的地方。

Splits

重头戏来了。

split 是对整个 node 的操作，因此需要修改 version（中的 vsplit），这样读操作就能意识到 split，避免脏读。这里的难点在于，修改是发生在写线程中，但检查是发生在读线程，需要正确处理，否则可能会有些修改生效了但没被读请求察觉。

split 过程中会手递手（hand-over-hand）标记和加锁：节点会自底向上标记为 “splitting” 和加锁。同时读请求会自顶向下检查 version。

考虑下面的中间节点 B 分裂出 B’ 的场景：

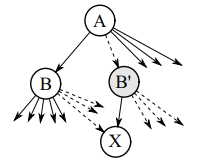
  1. B 和 B’ 标记为 splitting
  2. 包括 X 在内的一半子节点从 B 迁移到 B’
  3. A 被锁住，并标记为 inserting
  4. 将 B’ 插入 A
  5. 增加 A 的 vinsert、B 和 B’ 的 vsplit，并依次 unlock B，B’，A（按加锁顺序解锁）

为什么不能按加锁的逆序解锁？似乎也没什么问题

接下来作者探讨了 findborder 是如何与 split 配合保证正确性的。其核心思想就是与 hand-over-hand locking 相对应，findborder 中也要 hand-over-hand validate。对中间节点 A，要先获取 B/B’（取决于 findborder 的调用时机）的 version，再 double check A 并未处于 locked 状态，且这期间 A 并未发生分裂。因为是先获取 B/B’ 的 version，且通过 stableversion 我们知道这个时候 B/B’ 一定未处于 inserting 或 splitting 状态，因此此时要么 B/B’ 在一次 split 开始前，那我们就可以继续往下走；要么在我们获取之后 B/B’ 开始了一次 split，那接下来下一轮迭代时我们检查 B/B’ 的 version 就会 fail。

注意 Masstree 中 insert 总是原地重试，而 split 则会从 root 开始重试。一个因素是并发 split 比并发 insert 更为罕见（fanout 为 15，因此 insert 频率是 split 的 15 倍），因此可以用开销大一些的实现方式。

另一方面，insert 本身也要比 split 轻量很多，后者需要自底向上改变树的结构。

Border node 的 split 主要靠 border nodes 之间的链表来处理，有以下不变量：

  1. 每个 B+tree 初始只有一个 border node，这个 border node 永远不会被删除，且永远是最左边的 border node（链表头）。
  2. 每个 border node 负责的范围是 [lowkey, highkey)，其中 lowkey 永远不变，highkey 会在 split 和 delete 时修改。

注意一旦查找到达了某个 border node，就不再需要返回 root 进行重试了：顺着链表一路往下找就行了。

Removes

Remove 需要注意的几点：

  1. 不会物理删除 key-value，只会修改 permutation。这一步不需要修改 version。
  2. 但下次 insert 重用已标记删除的位置时，需要修改 vinsert 以避免脏读。
  3. border node 变为空时会被整个删除，因此我们需要维护一个双向链表来实现 O(1) 的删除节点操作。
  4. 中间节点的删除操作也需要 hand-over-hand locking。
  5. 一个 B+tree 为空时可以删除整个树，但需要确保同时锁上自身和上层指向它的 border node。
  6. 所有删除操作都需要在 epoch reclamation 的保护下进行。

Values

Masstree 中需要保证 value 具有原子修改能力。因此大多数情况下 Masstree 中的 value 都会指向一块单独分配的内存，修改时通过 copy-on-write，再替换这个指针。

当然对于直接支持 atomic 的 value 就可以原地修改了。

Discussion

Masstree 中 lookup 的 30% 的开销来自 node 内部的 key lookup。Masstree 现在是用线性查找，相比二分查找，它的时间复杂度会略高一些，但局部性更好。Masstree 的测试显示在 Intel 处理器上线性查找会快 5% 左右。

另一个潜在优化是类似于 PLAM 的并行查找，通过重叠内存的 prefetch 来掩盖访问内存的延时，测试显示在 Intel 处理器上会提升多达 34% 的吞吐（但在 AMD 机器上没有什么效果）。