原文：Better bitmap performance with Roaring bitmaps

TL;DR

本文提出了一种 bitmap 压缩格式 Roaring，它使用自适应的两级索引结构，分别用 bitmap 保存 dense 数据、用数组保存 sparse 数据，由此在空间占用与常见操作性能之间取得了很好的平衡。

相比 trivial 的 bitset 实现，Roaring 在内存占用，以及超稀疏场景下的操作性能上都有着明显的优势。相比基于 RLE 的 WAH 和 Concise 两种格式，它在空间占用与操作性能上都有着明显的优势。

Roaring 属于是一看就觉得 make sense，早该如此的 idea。

Background

bitmap 属于是超经典数据结构了。我们对 bitmap 的要求有：

空间占用，可以按 bit per element 来衡量。
常见操作的性能：
1. union
2. intersect
3. n-th element
4. count

最 trivial 的 bitmap 实现就是各种语言基本都带的 bitset。它的缺点是空间占用与元素密度成反比，当元素非常稀疏时空间占用太大。

Roaring 之前最常用的高性能 bitmap 实现主要是基于 RLE（run-length encoding）的，如 WAH 和 Concise。

WAH 将 n 位的 bitmap 按字长 w（如 32）位分成若干组。每组有两种类型：fill word 与 literal word：

fill word 指连续若干个 w-1 位都是相同的 0 或者 1，这样的序列用一个 word 表示，其中最高位为 1，次高位为 0 或 1，其余 w-2 位编码序列长度。如序列长度为 2，表示后面 62 位都是 0 或 1。
literal word 指 w-1 位中既有 0 又有 1，这样的 word 最高位为 0，接下来是 w-1 位数据。

WAH 的问题是当编码稀疏集合时，如 {0, 2(w-1), 4(w-1), …}，平均每个元素要用 2w 位来编码。

第一个 word 要用来编码 0-31 位，其中有一个元素，所以是 literal word；第二个 word 要用来编码 32-61 位，全是 0，所以是 fill word。依次类推，每个元素对应一个 literal word 和一个 fill word，所以是 2w 位。

Concise 则针对这种场景做了一个优化，将空间占用降了一半。它将 fill word 中用于编码 run-length 的部分抽出了 log2(w) 位（w=32 时抽出 5 位）用来编码 p（0<= p < w)。语义是：

接下来 w-1 位中，只有第 p-1 位是 0/1，其它 w-2 位都是 1/0。
再后面跟着 r（r 为 run-length）个 fill word。
如果 p=0，则表示后面 r+1 个都是 fill word。

这样上面的稀疏集合就可以表示为 n 个 fill word，平均每个元素使用 w 位。

注意 Concise 只是对 w-1 位中有一个特异值的场景做了特殊优化。当有超过 1 个特异值时，这 w-1 位仍然会编码为 literal word。

但这些基于 RLE 的编码都有个问题：随机访问慢。如 n-th element 需要 O(n) 时间。另外在做 union 或 intersection 操作时，如果遇到大段的 0 或 1，WAH 和 Concise 缺乏跳过另一个集合中对应范围的能力（需要跳到某个位置）。

实际上 RLE 编码普遍可以通过额外维护一个 index 来将 n-th element 降到 O(1) 时间。作者也提到了 auxiliary index。这里轻描淡写有点不厚道。

Roaring 的思路来自 RIDBit，两者都是将集合空间 [0, n) 分成若干个 chunk，每个 chunk 根据 dense 或 sparse 分别编码。两者区别在于 RIDBit 用链表来表达 sparse chunk，而 Roaring 则用紧凑的数组。众所周知链表对 cache 是非常不友好的，这点就造成了巨大的性能差异。

另外 Roaring 也应用了很多新的优化，其中比较重要的是依赖 CPU 的 popcnt 指令来快速计算 cardinality。

Roaring Bitmap

Roaring 的设计其实非常直接：

将 32 位整数的值域 [0, n) 分成长度为 2^16（64K）的 chunk。每个 chunk 中所有数字的高 16 位都相同。
chunk 中的元素数量不多于 4096 时，使用一个 16 位整数数组来保存每个元素的低 16 位。数组保持有序。元素数量多于 4096 时，用一个 2^16 位的 bitmap 表示所有元素。这样，我们总是能够保证平均每个元素占的空间不多于 16 位。
所有 chunk 的指针保存在一个动态数组中，按元素高 16 位排序。通常这个数组的 chunk 数量会很小，可以保持在 cache 中。

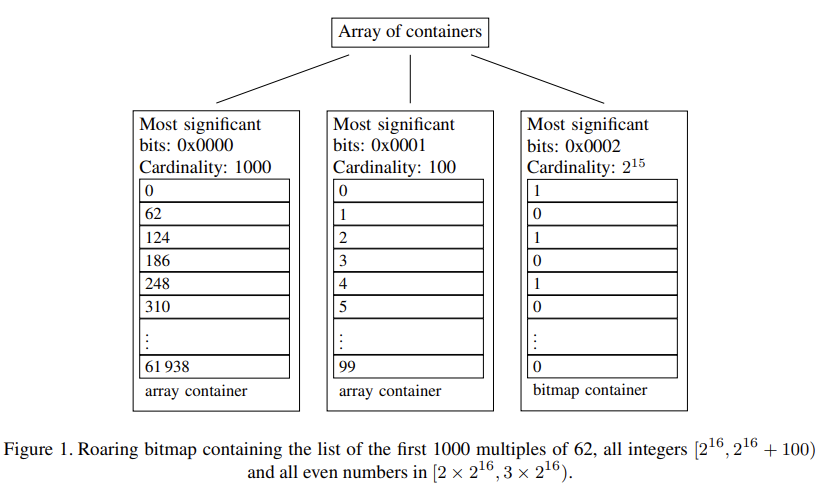
图中可以看到，每个 chunk 还会记录一些元数据：

高 16 位
cardinality

cardinality 可以用来加速 count、n-th element 等操作，在 union 和 intersection 等操作上也有帮助。

对于非常稠密的 chunk，如 cardinality >= 2^16-4096，Roaring 还可以将其转换为相反值对应的稀疏 chunk。

无论是 bitmap 还是 array 类型的 chunk，都还可以进一步应用 bitmap 或 array 上的一些编码方式，进一步降低空间或提升性能。

Access Operations

向一个 array chunk 插入新元素可能令其 cardinality 超过 4096，此时 Roaring 会将其转换为 bitmap chunk。相反 bitmap chunk 也会因删除元素被转换为 array chunk。

但直接用 4096 作为阈值可能产生颠簸，可能需要再选择一个阈值，比如 8192 作为 array chunk 到 bitmap chunk 的转换阈值。

array chunk 的插入和删除成本可能会很高（但有界，毕竟 size 不超过 4096）。

Logical Operations

这节主要讲 union 和 intersection 的实现。

Roaring 中两个集合做 union 或 intersection 时，总是先按高 16 位对齐 chunk，再对相应的两个 chunk 做 union 或 intersection，生成新 chunk（后面也讨论了 in-place 修改）。

接下来，我们根据两个 chunk 的类型分成三种情况讨论。

Bitmap vs Bitmap

每个 bitmap 大小为 2^16 位，因此两个 bitmap 之间的与或操作就等同于 1024 个 64 位整数之间的与或。

Algorithm 1 Routine to compute the union of two bitmap containers

1: input: two bitmaps A and B indexed as arrays of 1024 64-bit integers
2: output: a bitmap C representing the union of A and B, and its cardinality c
3: c ← 0
4: Let C be indexed as an array of 1024 64-bit integers
5: for i ∈ {1, 2, . . . , 1024} do
6:   Ci ← Ai OR Bi
7:   c ← c + bitCount(Ci)
8: return C and c

作者表示这里维护 cardinality 的代价并不大，原因：

bitCount 在现代 CPU 上直接映射为一条 popcnt，性能非常高，只需要一个周期。
对于现代的超标量 CPU，同时间可以有多条没有数据依赖的指令同时执行。上图中的 L6 和 L7 相互没有数据依赖，因此大概率是同时执行的。
这种简单运算的瓶颈通常是 cache miss，而不是运算能力。

作者的数据是 Java 下单线程每秒可以运算 7 亿次 64 位整数的或操作。如果加上 L7，吞吐降到了 5 亿次，下降了 30%，但仍然远高于 WAH 和 Concise。

上面是 union。对于 intersection，Roaring 将 cardinality 提前计算出来。如果新的 cardinality 不超过 4096，就会新生成一个 array，具体算法见 Algorithm 3，其中用 Algorithm 2 加速运算。

Algorithm 2 Optimized algorithm to convert the set bits in a bitmap into a list of integers. We assume two-complement’s arithmetic. The function bitCount returns the Hamming weight of the integer.

1: input: an integer w
2: output: an array S containing the indexes where a 1-bit can be found in w
3: Let S be an initially empty list
4: while w != 0 do
5:   t ← w AND − w // clear all 1s but the least 1 in w
6:   append bitCount(t − 1) to S
7:   w ← w AND (w − 1) // clear the least 1
8: return S

Algorithm 3 Routine to compute the intersection of two bitmap containers. The function bitCount returns the Hamming weight of the integer.

 1: input: two bitmaps A and B indexed as arrays of 1024 64-bit integers
 2: output: a bitmap C representing the intersection of A and B, and its cardinality c if c > 4096 or an equivalent array of integers  otherwise
 3: c ← 0
 4: for i ∈ {1, 2, . . . , 1024} do
 5:   c ← c + bitCount(Ai AND Bi)
 6: if c > 4096 then
 7:   Let C be indexed as an array of 1024 64-bit integers
 8:   for i ∈ {1, 2, . . . , 1024} do
 9:     Ci ← Ai AND Bi
10:   return C and c
11: else
12:   Let D be an array of integers, initially empty
13:   for i ∈ {1, 2, . . . , 1024} do
14:     append the set bits in Ai AND Bi to D using Algorithm 2
15:   return D

Bitmap vs Array

intersection：遍历 array 中的每个元素，查询 bitmap。

union：复制一份 bitmap，再依次将 array 中每个元素插入到 bitmap 中。

Array vs Array

union：如果 cardinality 之和不超过 4096，直接 merge 两个数组；否则先将结果写入一个 bitmap，最终如果发现 cardinality 不超过 4096，再将 bitmap 转换回 array（使用 Algorithm 2）。

intersection：如果两个 array size 差距不那么悬殊（64 倍以上），则直接 merge，否则使用 galloping intersection 算法。

galloping intersection 是遍历小数组中每个元素，在大数组中二分查找。它要求输入两个数组大小差距非常悬殊。

以上所有操作也可以 in-place 修改，好处是避免了内存分配和初始化。

另外，当聚合非常多个 chunk 时，比如 union，我们可以先从中找到一个 bitmap，复制一份出来，再将其它 chunk 都原地 union 到这个复制的 bitmap 上。

Algorithm 4 Optimized algorithm to compute the union of many roaring bitmaps

 1: input: a set R of Roaring bitmaps as collections of containers; each container has a cardinality and a 16-bit key
 2: output: a new Roaring bitmap T representing the union
 3: Let T be an initially empty Roaring bitmap.
 4: Let P be the min-heap of containers in the bitmaps of R, configured to order the containers by their 16-bit keys.
 5: while P is not empty do
 6:   Let x be the root element of P. Remove from the min-heap P all elements having the same key as x, and call the result Q.
 7:   Sort Q by descending cardinality; Q1 has maximal cardinality.
 8:   Clone Q1 and call the result A. The container A might be an array or bitmap container.
 9:   for i ∈ {2, . . . , |Q|} do
10:     if A is a bitmap container then
11:       Compute the in-place union of A with Qi: A ← A OR Qi. Do not re-compute the cardinality of A: just compute the bitwise-OR operations.
12:     else
13:       Compute the union of the array container A with the array container Qi: A ← A OR Qi. If A exceeds a cardinality of 4096, then it beco  mes a bitmap container.
14:   If A is a bitmap container, update A by computing its actual cardinality.
15:   Add A to the output of Roaring bitmap T.
16: return T

Experiments

一图胜千言