0%

数据丢失概率与节点数量的关系

发表于 更新于

TL;DR

分布式系统中我们经常会使用多副本策略来保证数据的可靠性。常见的多副本策略可以按容错能力分为两类。假设系统需要能容忍最多 f 个节点失败：

  1. 需要 2f+1 个副本的 Quorum 策略，如 Paxos/Raft
  2. 需要 f+1 个副本，如 chain replication（下文称 CR）。

本文通过简单的模拟计算，得到以下结论：

  1. 固定节点失败概率与每个节点上的 shard 数量，数据丢失概率是节点数量的凸函数，即随着节点数量增加，数据丢失概率逐渐增大，到达峰值后再逐渐减小。
  2. 同等存储成本下，CR 的数据丢失概率远低于 Quorum。

我们假设节点失败概率为 P，每个节点上有 K 个 shard，每个 shard 有 3 个副本。对于 Quorum，shard 容忍最多一个副本失败。对于 CR，shard 容忍最多两个副本失败。

数据丢失可以被定义为：当有超过 f 个节点同时失败，且存在 shard 恰好有超过 f 个副本位于这些节点上。这样我们可以将数据丢失概率计算为以下两个概率的乘积：

  1. 超过 f 个节点同时失败的概率。
  2. 存在 shard 恰好有超过 f 个副本位于这些节点的概率。

前者我们记为 Pn，后者记为 Ps。为了简化计算，下面我们只计算 shard 恰好有 f+1 个副本位于这些节点的概率。且记 Pss 为一个 shard 发生数据丢失的概率。则 Ps = (1-Pss)NK。

对于Quorum，f = 1，则发生了超过 2 个节点失败，且有 shard 有 2 个副本位于其上的概率为：

  • Pn = Pn = 1 - (1-P)n - C(N, 1) * P(1-P)N-1
  • Pss = C(2, 2) * C(N-2, 1) / C(N, 3)
  • Ps = (1-Pss)NK
  • Pres = Pn * Ps

对于 CR，f = 2，则发生了超过 3 个节点失败，且有 shard 有 3 个副本位于其上的概率为：

  • Pn = 1 - (1-P)n - C(N, 1) * P(1-P)N-1 - C(N, 2) * P2(1-P)(N-2)，其中分别减掉了：
    • 所有节点都正常的概率
    • 只有一个节点失败的概率
    • 只有两个节点失败的概率
  • Pss = C(3, 3) / C(N, 3)
  • Ps = (1-Pss)NK
  • Pres = Pn * Ps

以上对于 Pss 的计算做了一些简化，但不影响结论。

可以看到 Pn 是关于 n 的单调增函数，而 Ps 则是关于 n 的单调减函数。

接下来直接上图。

Quorum

P = 0.001，K = 1000

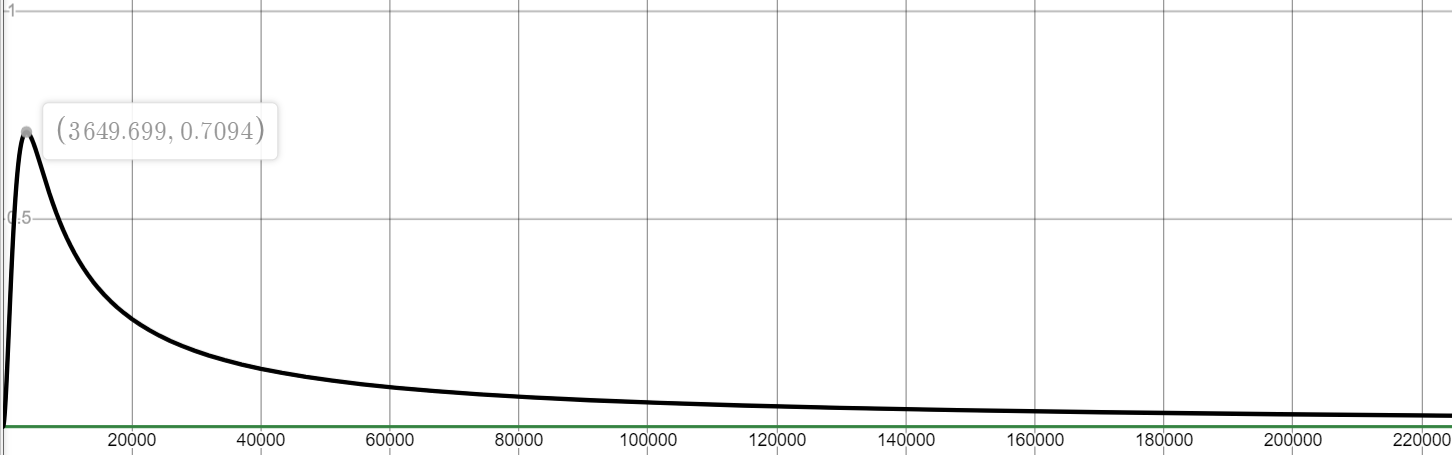
P = 0.001，K = 5000

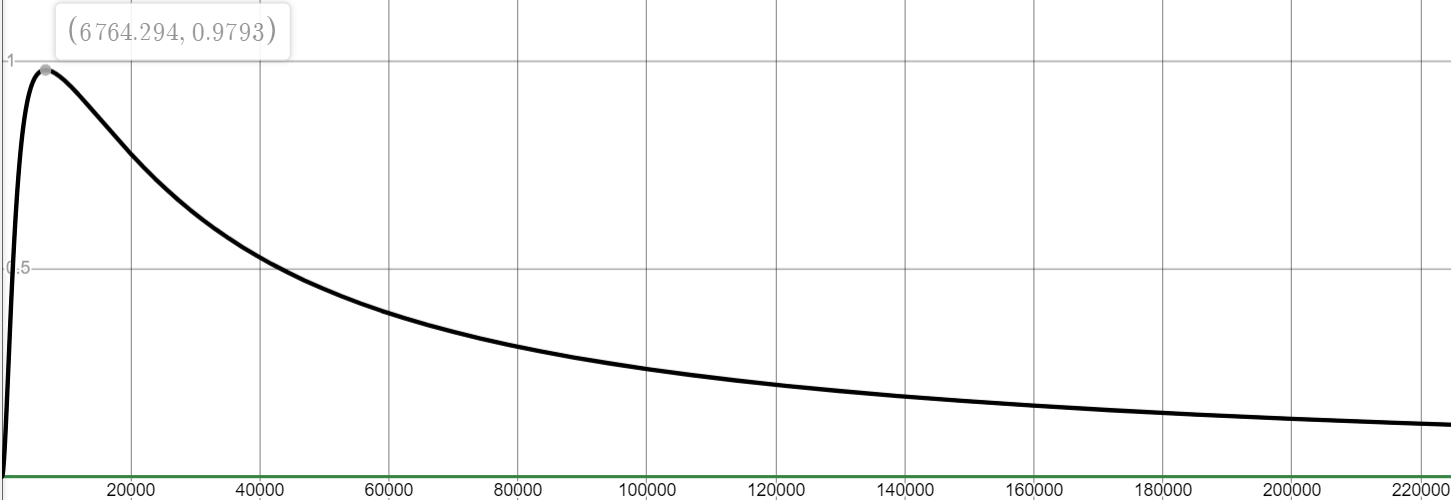
P = 0.0001，K = 5000

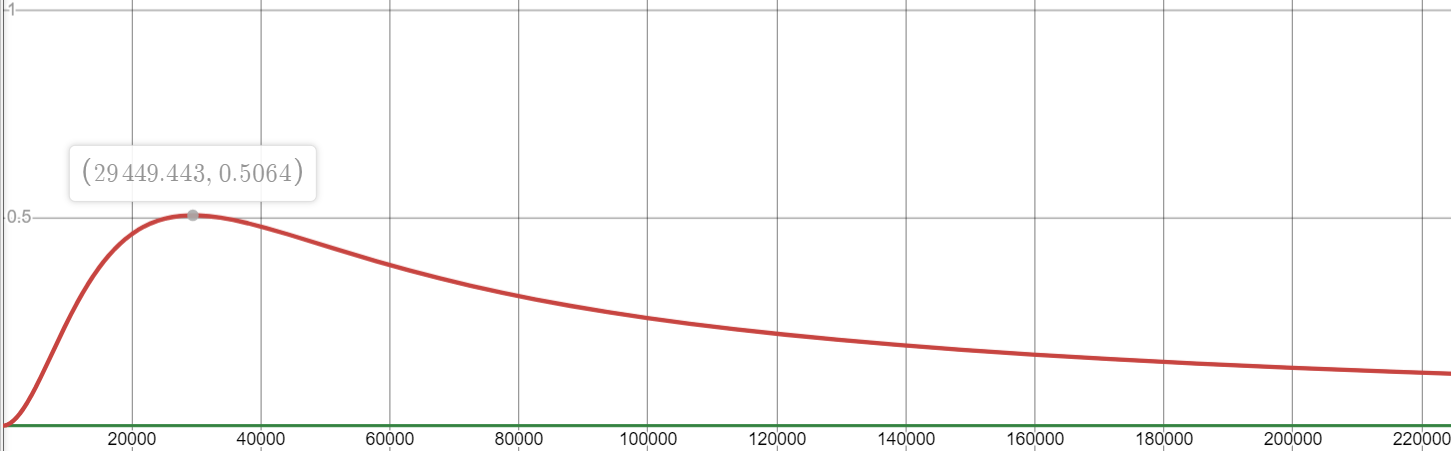
P = 0.00001，K = 5000

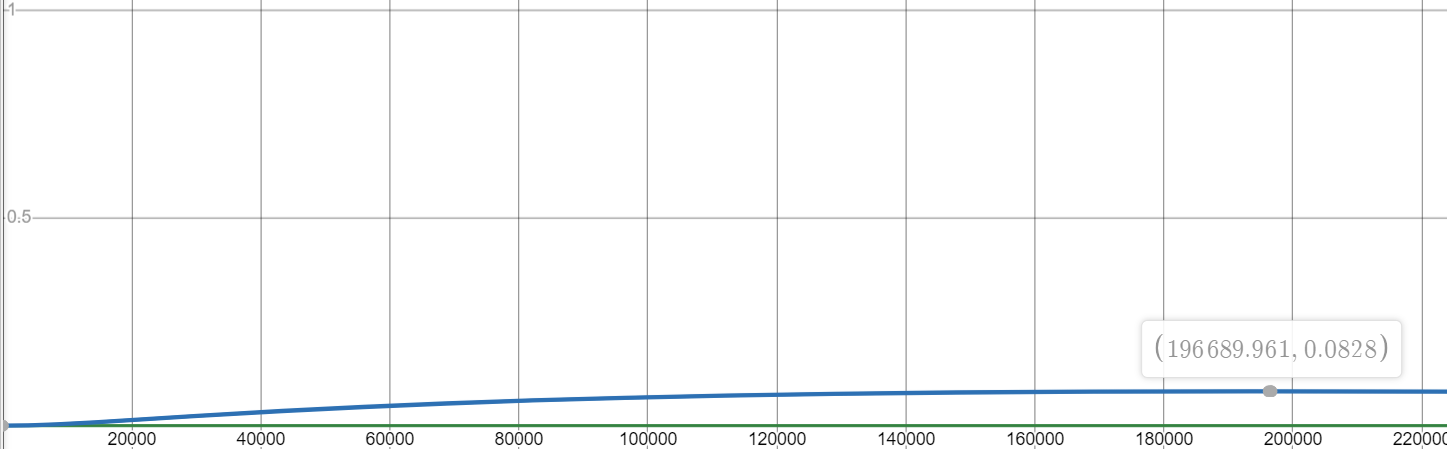
Chain replication（注意 Y 轴）

P = 0.001，K = 1000

P = 0.001，K = 5000

P = 0.0001，K = 5000

P = 0.00001，K = 5000

可以看到：

  1. 随着节点数量增加，数据丢失概率先增大后减小。
  2. 同样 3 副本，CR 因为可以容忍 2 副本失败，相同参数下数据丢失概率远小于 Quorum。

如果我们将 CR 设置为 2 副本，因此同样容忍 1 副本失败（但更省存储空间），此时 Pn 与 Quorum 相同，而 Pss = C(2, 2) / C(N, 2)，小于 Quorum。

P = 0.001，K = 1000

P = 0.00001，K = 5000

可以看到，CR 用更少的存储空间实现了更低的数据丢失概率。

启示：

  1. 只考虑存储空间与数据可靠性的话，Chain replication 相比 Quorum（Paxos/Raft）更适合用于数据平面。
  2. 在集群节点数量增加时，需要考虑是否有必要增加副本数量。

上述结论与数据分布无关，如 Copyset 等策略相当于降低了 Pss，正交于具体的共识算法。

安利一个网站：https://www.desmos.com/calculator