原文:Chord: A Scalable Peer-to-Peer Lookup Protocol for Internet Applications
TL;DR
Chord解决的是P2P系统(去中心化)中如何高效确定数据位置的问题。
P2P系统中最常见的方案是将数据按一致性hash分散到不同节点上,这样显著减少了节点增减时产生的数据迁移。这套方案中最重要的是每个节点需要维护一个路由表,在接收到请求时,如果数据不在自己上面,需要根据路由表将请求转发给对应的节点。传统的一致性hash里路由表需要包含全部节点信息,产生了O(N)的维护代价,规模大了就会有问题。
Chord在一致性hash基础上,只需要每个节点维护O(logN)大小的路由表,同样能实现O(logN)的查找,即使路由信息过时了也能回退到O(n)查找。减少了路由表的大小,显著地降低了Chord的维护代价,能在节点不停变化时仍然保持不错的性能。
Dynamo似乎使用了类似Chord的方案。
Chord的前提:
- 节点间数据按一致性hash分布,可以使用虚拟节点。
假设网络是:
- 对称的(如果A能访问B,则B也能访问A)。
- 可传递的(如果A能访问B,B能访问C,则A也能访问C)。
(真实网络不是这样的,此时需要有其它协议做错误检测并踢掉导致网络问题的节点,如Cassandra使用的The ϕ Accrual Failure Detector)
定理4.1:对于任意N个节点和K个key,以下大概率成立:
- 每个节点负责最多(1+ε)K/N个key。
- 节点N+1加入或离开会导致O(K/N)个key发生迁移(到或出这个节点)。
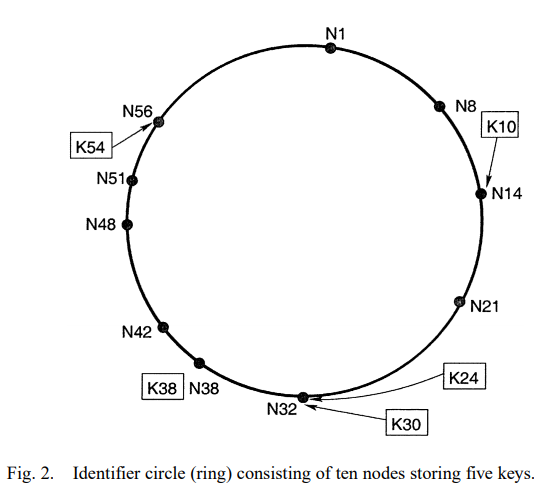
在这样的环上查找时,每个节点最少只需要知道它的下家(successor)是谁,此时就是线性查找。
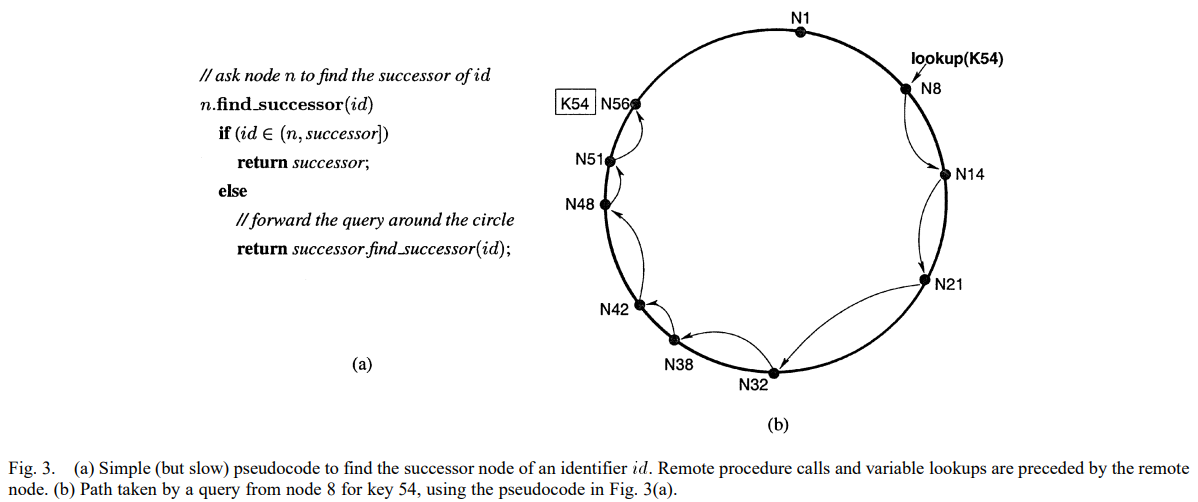
接下来每个节点要维护的信息变成了一个finger table,其中包含最多O(logm)项(m是hash最大值),每项记录base+2i-1的位置(1<=i<=m),这样就可以以O(logN)的时间复杂度完成查找(此时整个环类似于一个skiplist)。
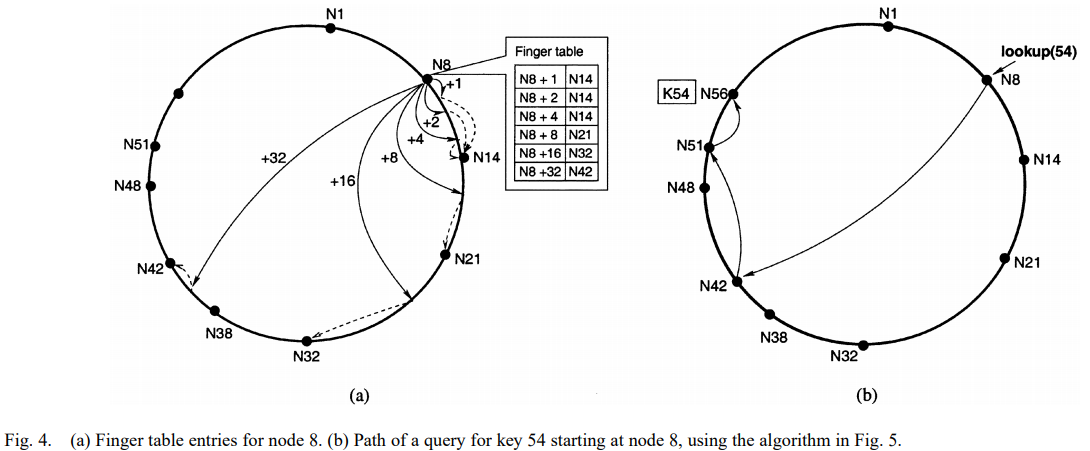

定理4.2:N个节点的Chord网络中,find_successor要通信的节点数大概率是O(logN)。
接下来我们看Chord怎么处理节点的加入和离开。
为了保证finger table不过时,每个节点会定期执行“stabilization”以更新finger table和successor/predecessor。

新节点join后还不会立即进入Chord环,以及其它节点的finger table,随着后续的stabilization,最终会被识别并加入。
定理4.3:任意的join与stabilization交错执行后,所有节点的successor会在某个时间构成完整的。
注意stabilization无法处理整个环分裂为多个环的情况,不过正常的join/leave不会导致这种情况的发生。
接下来考虑stabilization之前的查找,有三种可能:
- finger table不需要修改,指向正确的位置。这是最可能的情况,此时正确性和性能都不是问题。
- finger table不准确,但successor正确,此时正确性不是问题,但性能会有一定的退化。
- successor也不正确,或对应数据还没做完迁移,此时可能查找不到数据,上层应用要考虑等待一段时间再重试。
定理4.4:假设有N个节点的稳定(finger table和successor都正确)网络,此时再加入最多N个节点,保证所有successor指针正确(但不保证finger table正确),则查找仍然大概率需要O(logN)次跳转。
接下来我们考虑节点fail的情况。
Chord协议的正确性依赖于每个节点的successor指针正确,但当有节点fail了,如图4中节点14、21、32都fail的话,节点8的successor应该是节点38,但它的finger table里没有节点38,此时查找就会失败。比如节点8要查找30,就会转发给节点42。
Chord的对策是每个节点除了finger table外,还维护下面r个successor,当直接successor不响应的时候,节点就依次询问successor列表中后面的节点。只有当r个全失败了才会导致查找失败。
维护successor list的方式是定期获取直接successor的successor list,将它加进去,再踢掉最后一个。
有了successor list后,图5中的closest_preceding_node就会同时考虑finger table和successor list了。
定理4.5:在一个初始稳定的网络中,如果successor list长度r = Ω(logN),之后每个节点有50%概率失败,则大概率find_successor仍然能返回正确的节点。
定理4.6:在一个初始稳定的网络中,如果每个节点的失败概率为50%,则find_successor的预期执行时间仍然为O(logN)。
successor list还可以被上层应用用来实现replication(如Dynamo)。
节点离开可以不走失败的处理路径,而是主动迁移数据并告知它的successor/predecessor,这样就能显著降低节点离开的影响。
当然现实场景中Chord系统可能永远无法处于稳定状态,但有研究表明只要stabilization以合理的频率运行,Chord环仍然能以几乎稳定的状态运行,并保证正确性和性能。
接下来我们看如何改进路由的延时。
考虑到地域因素,尽管一次路由的通信数可以保证在(1/2)logN,但延时可能会很大:环上相近的节点现实中可能距离很远。
作者之前的一个idea是在构建finger table时同时考虑环上距离和现实中的延时,但这种方案的性能很难评估。
这里作者的idea是每个finger维护多个节点,并维护与它们的通信延时,在路由时尽量发请求给延时最低的节点。
最后作者讨论了如何维护Chord环的一致性,误操作、bug、恶意节点都可能导致Chord环分裂。一种方案是每个节点x定期在环上查找自己负责范围内的key y,如果找不到,或结果不是x,说明一致性可能被破坏了。